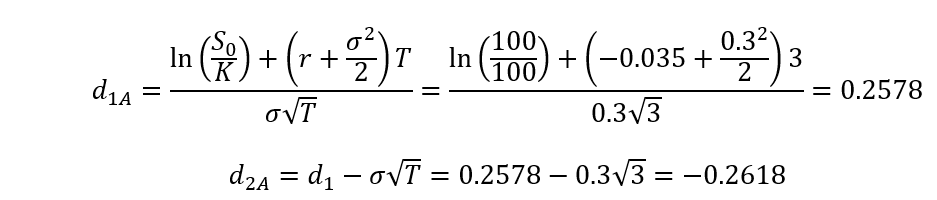The History Of Options Contracts
The Black-Scholes-Merton formula became immediately the gold-standard in option pricing, both in academia and in the financial industry.1. It all started with Olives!
The anecdotal evidence about financial tools resembling options can be traced back to at least 580 B.C.. According to a story in Politics by Aristotle, Thales of Miletus bought, with a small deposit, the rights to use the olive presses in Chios and Miletus, just ahead of the olive harvest. The nature of the contract implied the right but not the obligation to use the presses and was subject to a premium, in the form of the deposit. This effectively made such a contract a call option.
Unfortunately, we do not know what price Thales of Miletus paid for its contract. What we know, however, is that it would take slightly less than 2 500 years before a formal model for pricing contracts such as the one by Thales of Miletus would be widely available to everyone. The documentary Trillion Dollar Bet guides us in the origins, development of this model, the Black-Scholes-Merton model, together with its rationale, its consequences and its drawbacks.


2. The Brownian motion theory in 1900’s
The debate about whether skill or luck can explain success in the financial markets is perhaps old as the financial markets themselves. However, it is only at the beginning of the 20th century that economists and financial academics begun to treat and model possible answers to this research question using formal mathematics. One of the pioneers of this framework was a French economist, Louis Bachelier, who in his dissertation thesis Théorie de la speculation in 1900 compared the behavior of buyers and sellers on the markets to the random movement of physical particles suspended in fluid. Using equations, Bachelier created the first simulation of the stock market prices fluctuations. Bachelier was convinced that asset prices in financial markets developed randomly and it was therefore impossible to predict them. Importantly, Bachelier focused not only on returns but also on risk; he arrived to the conclusion that risk can be mastered in financial markets through the use of options. Bachelier realized options could protect investors from market fluctuations and made the first attempt to figure out how to price them. Sadly, Bachelier’s accomplishment would go unnoticed for decades.
3. Revisted attempt in the 50’s
Bachelier’s work was however rediscovered in the 1950’s by Paul Samuelson, the first American to win the Nobel Memorial Prize in Economic Sciences in 1970. Following the work by Samuelson, more and more economists and traders became attracted by Bachelier’s ideas and, in turn, this helped to popularize options as a financial tool to manage risk. As the popularity of options as an insurance and leverage tool grew bigger, the need of a widespread and standardized option pricing model become more and more acute.
To address such a need, leading economists worldwide created new models based on micro-foundations, that is, on the theory of how a single individual behaves, her/his risk aversion, objectives and preferences. By the late 1960, however, an option pricing model did not still exist. This was about to change.

4. The model today
In 1968, economists Myron Scholes and Fisher Black set up to tackle the problem of options. They started from the evidence that the price of an option and the price of the options’ underlying asset were moving together. At first, a formula which would yield one-to-one map of the underlying value into the option’s value was elusive for the researchers. Neither a massive review of the literature helped, as in the words of Scholes, the previous literature made use of unsatisfying assumptions.
At that point they decided to take their by-then basic model and eliminate all the variables that were not measurable. To their surprise, this did not affect the calculations. Nevertheless, the researchers were left with one parameter – risk – that they were still unable to remove from the model. To circumvent this problem, the researchers gave rise to a revolutionary assumption: dynamic hedging. Dynamic hedging implies hedging of one’s bet by taking the bet’s opposite positions, theoretically, every instant of time. Every movement of one’s financial position is, in this way, smoothed out as the positions of one’s portfolio cancel each other out. With the help of a third researcher, Merton, and Ito’s calculus to practically implement dynamic hedging, this was the perfect solution that enabled the researchers to drop the risk out of the option pricing equation.
This scientific breakthrough was the final step to the simple and wonderful equation that characterize the Black-Scholes-Merton model and that is here illustrated:

In eq. (1), C stands for the price of a call option, S(0) is the initial price of the option’s underlying asset, K is the option’s Strike Price, r is the risk-free rate, T is the time to maturity, N(d1) and N(d2) are cumulative probability distribution functions for a variable with a standard Normal distribution.
The Black-Scholes-Merton formula became immediately the gold-standard in option pricing, both in academia and in the financial industry.
Further reading
The History Of Options Contracts
The anecdotal evidence about financial tools resembling options can be traced back to at least 580 B.C.
Watch Trillion Dollar Bet (2000)
Watch the documentary on the Black-Scholes option pricing.
Black-Scholes formula with example
The Anatomy of the Black-Scholes-Merton formula.
Test our Black & Scholes calculator
We created a fun and educational Black & Scholes calculator for you to use for free!
17 Equations that Changed the World
From Newton's Law of Gravity to the Black-Scholes model used by bankers to predict the markets, equations, are everywhere - and they are fundamental to everyday life.