The Anatomy of the Black-Scholes-Merton formula
This article gives you a background to the famous option pricing formula
The Black-Sholes-Merton formula for a call option reads as follows:

where C stands for the price of a call option, S(0) is the initial price of the option’s underlying asset, K is the option’s Strike Price, r is the risk-free rate, T is the time to maturity. N(d1) and N(d2) are cumulative probability distribution functions for a variable with a standard Normal distribution, which are specified as follows:

Let us now take a practical example of how the Black-Scholes-Merton formula can be used to calculate the price of the Option A in our presentation. The Option A is European Long Call and has the following characteristics:
Asset price (S0)
Strike Price (K)
Time-to-maturity in years (T)
Interest Rate (e^(-rT)
Volatility (σ)
As a first step, let us proceed to calculate eqs. (2) and (3):
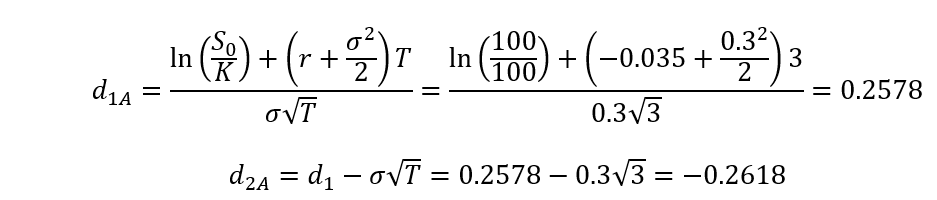

Further reading
More articles on the same topicThe History Of Options Contracts
The anecdotal evidence about financial tools resembling options can be traced back to at least 580 B.C.
Watch Trillion Dollar Bet (2000)
Watch the documentary on the Black-Scholes option pricing.
Black-Scholes formula with example
The Anatomy of the Black-Scholes-Merton formula.
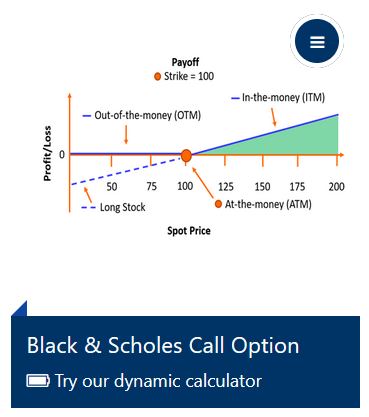
Test our Black & Scholes calculator
We created a fun and educational Black & Scholes calculator for you to use for free!
17 Equations that Changed the World
From Newton's Law of Gravity to the Black-Scholes model used by bankers to predict the markets, equations, are everywhere - and they are fundamental to everyday life.